Cinemática
Unidad # 3
Mi opinión :
La cinemática es la rama de la física que estudia las leyes del movimiento de los cuerpos sin considerar las causas que lo originan (las fuerzas) y se limita, esencialmente, al estudio de la trayectoria en función del tiempo. La aceleración es el ritmo con el que cambia la velocidad. La velocidad y la aceleración son las dos principales magnitudes que describen cómo cambia la posición en función del tiempo.
Movimiento rectilíneo
Es aquél en el que el móvil describe una trayectoria en línea recta.
Movimiento rectilíneo uniforme
En este movimiento la velocidad permanece constante y no hay una variación de la aceleración (a) en el transcurso del tiempo. Esto corresponde al movimiento de un objeto lanzado en el espacio fuera de toda interacción, o al movimiento de un objeto que se desliza sin fricción. Siendo la velocidad v constante, la posición variará lineal mente respecto del tiempo, según la ecuación
Movimiento armónico simple
Es un movimiento periódico de vaivén, en el que un cuerpo oscila a un lado y a otro de una posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. Matemáticamente, la trayectoria recorrida se expresa en función del tiempo usando funciones trigonométricas, que son periódicas. Así por ejemplo, la ecuación de posición respecto del tiempo, para el caso de movimiento en una dimensión
la que corresponde a una función sinusoidal de frecuencia f \,, de amplitud A y fase de inicial \phi \,.
Los movimientos del péndulo, de una masa unida a un muelle o la vibración de los átomos en las redes cristalinas son de estas características.
La aceleración que experimenta el cuerpo es proporcional al desplazamiento del objeto y de dirección contraria, desde el punto de equilibrio. Matemáticamente:
donde k \, es una constante positiva y x \, se refiere a la elongación (desplazamiento del cuerpo desde la posición de equilibrio).
La solución a esa ecuación diferencial lleva a funciones trigonométricas de la forma anterior. Lógicamente, un movimiento periódico oscilatorio real se ralentiza en el tiempo (por fricción mayormente), por lo que la expresión de la aceleración es más complicada, necesitando agregar nuevos términos relacionados con la fricción. Una buena aproximación a la realidad es el estudio del movimiento oscilatorio amortiguado
Movimiento parabólico
El movimiento parabólico se puede analizar como la composición de dos movimientos rectilíneos distintos: uno horizontal (según el eje x) de velocidad constante y otro vertical (según eje y) uniformemente acelerado, con la aceleración gravitatoria; la composición de ambos da como resultado una trayectoria parabólica.
Claramente, la componente horizontal de la velocidad permanece invariable, pero la componente vertical y el ángulo θ cambian en el transcurso del movimiento.
En la figura 4 se observa que el vector velocidad inicial \ v_0 forma un ángulo inicial \ \theta_0 respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:
El desplazamiento horizontal está dado por la ley del movimiento uniforme, por tanto sus ecuaciones
En tanto que el movimiento según el eje \ y será rectilíneo uniformemente acelerado, siendo sus ecuaciones:
y representa una parábola en el plano y(x). En la figura 4 se muestra esta representación, pero en ella se ha considerado \ y_0=0 (no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad \ v_y sea nula (máximo de la parábola); y que el alcance horizontal \ x ocurrirá cuando el cuerpo retorne al suelo, en \ y=0 (donde la parábola corta al eje \ x ).
Movimiento circular

El movimiento circular en la práctica es un tipo muy común de movimiento: Lo experimentan, por ejemplo, las partículas de un disco que gira sobre su eje, las de una noria, las de las agujas de un reloj, las de las paletas de un ventilador, etc. Para el caso de un disco en rotación alrededor de un eje fijo, cualquiera de sus puntos describe trayectorias circulares, realizando un cierto número de vueltas durante determinado intervalo de tiempo. Para la descripción de este movimiento resulta conveniente referirse ángulos recorridos; ya que estos últimos son idénticos para todos los puntos del disco (referido a un mismo centro). La longitud del arco recorrido por un punto del disco depende de su posición y es igual al producto del ángulo recorrido por su distancia al eje o centro de giro. La velocidad angular (ω) se define como el desplazamiento angular respecto del tiempo, y se representa mediante un vector perpendicular al plano de rotación; su dirección se determina aplicando la "regla de la mano derecha" o del sacacorchos. La aceleración angular (α) resulta ser variación de velocidad angular respecto del tiempo, y se representa por un vector análogo al de la velocidad angular, pero puede o no tener la misma dirección (según acelere o retarde).
La velocidad (v) de una partícula es una magnitud vectorial cuyo módulo expresa la longitud del arco recorrido (espacio) por unidad de tiempo tiempo; dicho módulo también se denomina rapidez o celeridad. Se representa mediante un vector cuya dirección es tangente a la trayectoria circular y coincide con el del movimiento.
La aceleración (a) de una partícula es una magnitud vectorial que indica la rapidez con que cambia la velocidad respecto del tiempo; esto es, el cambio del vector velocidad por unidad de tiempo. La aceleración tiene generalmente dos componentes: la aceleración tangencial a la trayectoria y la aceleración normal a ésta. La aceleración tangencial es la que causa la variación del módulo de la velocidad (celeridad) respecto del tiempo, mientras que la aceleración normal es la responsable del cambio de dirección de la velocidad. Los módulos de ambas componentes de la aceleración dependen de la distancia a la que se encuentre la partícula respecto del eje de giro.
Movimiento circular uniforme
Se caracteriza por tener una velocidad variable o estructural constante por lo que la aceleración angular es nula. La velocidad lineal de la partícula no varía en módulo, pero sí en dirección. La aceleración tangencial es nula; pero existe aceleración centrípeta (la aceleración normal), que es causante del cambio de dirección.
Matemáticamente, la velocidad angular se expresa
La velocidad es la derivada temporal del vector de posición y la aceleración es la derivada temporal de la velocidad:

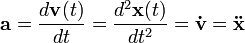
o bien sus expresiones integrales:


- EXISTEN DOS TIPOS DE MOVIMIENTO, CARACTERIZADOS POR SU TRAYECTORIA, DE ESTA CATEGORÍA:
- Magnitud física
Una magnitud física es una propiedad o cualidad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición o una relación de medidas. Las magnitudes físicas se miden usando un patrón que tenga bien definida esa magnitud, y tomando como unidad la cantidad de esa propiedad que posea el objeto patrón. Por ejemplo, se considera que el patrón principal de longitud es el metro en el Sistema Internacional de Unidades.
Las primeras magnitudes definidas estaban relacionadas con la medición de longitudes, áreas, volúmenes, masas patrón, y la duración de periodos de tiempo.
Existen magnitudes básicas y derivadas, y constituyen ejemplos de magnitudes físicas: la masa, la longitud, el tiempo, la carga eléctrica, la densidad, la temperatura, la velocidad, la aceleración y la energía. En términos generales, es toda propiedad de los cuerpos o sistemas que puede ser medida. De lo dicho se desprende la importancia fundamental del instrumento de medición en la definición de la magnitud.1
La Oficina Internacional de Pesos y Medidas, por medio del Vocabulario Internacional de Metrología (International Vocabulary of Metrology, VIM), define a la magnitud como un atributo de un fenómeno, un cuerpo o sustancia que puede ser distinguido cualitativamente y determinado cuantitativamente.2
A diferencia de las unidades empleadas para expresar su valor, las magnitudes físicas se expresan en cursiva: así, por ejemplo, la "masa" se indica con "m", y "una masa de 3 kilogramos" la expresaremos como m = 3 kg.
Magnitudes escalares, vectoriales y tensoriales
Las magnitudes escalares son aquellas que quedan completamente definidas por un número y las unidades utilizadas para su medida. Esto es, las magnitudes escalares están representadas por el ente matemático más simple, por un número. Podemos decir que poseen un módulo, pero que carecen de dirección. Su valor puede ser independiente del observador (v.g.: la masa, la temperatura, la densidad, etc.) o depender de la posición (v.g.: la energía potencial), o estado de movimiento del observador (v.g.: la energía cinética).
Las magnitudes vectoriales son aquellas que quedan caracterizadas por una cantidad (intensidad o módulo), una dirección y un sentido. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa mediante un segmento orientado. Ejemplos de estas magnitudes son: la velocidad, la aceleración, la fuerza, el campo eléctrico, intensidad luminosa, etc.
Además, al considerar otro sistema de coordenadas asociado a un observador con diferente estado de movimiento o de orientación, las magnitudes vectoriales no presentan invariancia de cada uno de los componentes del vector y, por tanto, para relacionar las medidas de diferentes observadores se necesitan relaciones de transformación vectorial. En mecánica clásica también el campo electrostático se considera un vector; sin embargo, de acuerdo con la teoría de la relatividad esta magnitud, al igual que el campo magnético, debe ser tratada como parte de una magnitud tensorial.
Las magnitudes tensoriales son las que caracterizan propiedades o comportamientos físicos modelizables mediante un conjunto de números que cambian tensorialmente al elegir otro sistema de coordenadas asociado a un observador con diferente estado de movimiento (marco móvil) o de orientación.
De acuerdo con el tipo de magnitud, debemos escoger leyes de transformación (por ej. la transformación de Lorentz) de las componentes físicas de las magnitudes medidas, para poder ver si diferentes observadores hicieron la misma medida o para saber qué medidas obtendrá un observador, conocidas las de otro cuya orientación y estado de movimiento respecto al primero sean conocidos.
Magnitudes extensivas e intensivas
Una magnitud extensiva es una magnitud que depende de la cantidad de sustancia que tiene el cuerpo o sistema. Las magnitudes extensivas son aditivas. Si consideramos un sistema físico formado por dos partes o subsistemas, el valor total de una magnitud extensiva resulta ser la suma de sus valores en cada una de las dos partes. Ejemplos: la masa y el volumen de un cuerpo o sistema, la energía de un sistema termodinámico, etc.
Una magnitud intensiva es aquella cuyo valor no depende de la cantidad de materia del sistema. Las magnitudes intensivas tiene el mismo valor para un sistema que para cada una de sus partes consideradas como subsistemas. Ejemplos: la densidad, la temperatura y la presión de un sistema termodinámico en equilibrio.
En general, el cociente entre dos magnitudes extensivas da como resultado una magnitud intensiva. Ejemplo: masa dividida por volumen representa densidad.
Representación covariante y contravariante
Las magnitudes tensoriales de orden igual o superior a uno admiten varias formas de representación tensorial según el número de índices contravariantes y covariantes. Esto no es muy importante si el espacio es euclídeo y se emplean coordenadas cartesianas, aunque si el espacio no es euclídeo o se usan coordenadas no cartesianas es importante distinguir entre diversas representaciones tensoriales que físicamente representan la misma magnitud. En relatividad general dado que en general el espacio-tiempo es curvo el uso de representaciones convariantes y cotravariantes es inevitable.
Así un vector puede ser representado mediante una tensor 1-covariante o mediante un tensor 1-contravariante. Más generalmente, una magnitud tensorial de orden k admite 2k representaciones tensoriales esencialmente equivalentes. Esto se debe a que en un espacio físico representable mediante una variedad riemanniana (o semiriemanninana como en el caso relativista) existe un isomorfismo entre tensores de tipo \scriptstyle (m,n) y los de tipo \scriptstyle (m',n') siempre y cuando \scriptstyle m+n = m'+n'. El paso de una representación a otra de otro tipo se lleva a cabo mediante la operación de "bajar y subir índices".
Magnitudes objetivas y no objetiva
Una magnitud se dice objetiva si las medidas de dicha magnitud por observadores diferentes pueden relacionarse de manera sistemática. En el contexto de la mecánica newtoniana se restringe el tipo de observador, y se considera que una magnitud es objetiva si se pueden relacionar sistemáticamente las medidas de dos observadores cuyo movimiento relativo en un instante dado es un movimiento de sólido rígido. Existen buenos argumentos para sostener que una ley física adecuada debe estar formulada en términos de magnitudes físicas objetivas. En el contexto de la teoría de la relatividad la objetividad física se amplia al concepto de covariancia de Lorentz (en relatividad especial) y covariancia general (en relatividad especial).
Sistema Internacional de Unidades
Artículo principal: Sistema Internacional de Unidades
El Sistema Internacional de Unidades se basa en dos tipos de magnitudes físicas:
Las siete que toma como unidades fundamentales, de las que derivan todas las demás. Son longitud, tiempo, masa, intensidad de corriente eléctrica, temperatura, cantidad de sustancia e intensidad luminosa.
Las unidades derivadas, que son las restantes y que pueden ser expresadas con una combinación matemática de las anteriores.
Unidades básicas o fundamentales del Sistema Internacional de Unidades[editar · editar código]
Artículo principal: Unidades básicas del SI
Las magnitudes básicas no derivadas del SI son las siguientes:
Longitud: metro (m). El metro es la distancia recorrida por la luz en el vacío en 1/299 792 458 segundos. Este patrón fue establecido en el año 1983.
Tiempo: segundo (s). El segundo es la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del cesio-133. Este patrón fue establecido en el año 1967.
Masa: kilogramo (kg). El kilogramo es la masa de un cilindro de aleación de Platino-Iridio depositado en la Oficina Internacional de Pesas y Medidas. Este patrón fue establecido en el año 1887.
Intensidad de corriente eléctrica: amperio (A). El amperio o ampere es la intensidad de una corriente constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno de otro, en el vacío, produciría una fuerza igual a 2×10-7 newton por metro de longitud.
Temperatura: kelvin (K). El kelvin es la fracción 1/273,16 de la temperatura del punto triple del agua.
Cantidad de sustancia: mol (mol). El mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 12 gramos de carbono-12.
Intensidad luminosa: candela (cd). La candela es la unidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540×1012 Hz y cuya intensidad energética en dicha dirección es 1/683 vatios por estereorradián.
Unidades Fundamentales en el Sistema Cegesimal C.G.S.[editar · editar código]
Artículo principal: Sistema Cegesimal de Unidades
Longitud: centímetro (cm): 1/100 del metro (m) S.I.
Tiempo: segundo (s): La misma definición del S.I.
Masa: gramo (g): 1/1000 del kilogramo (kg) del S.I.
Unidades Fundamentales en el Sistema Gravitacional Métrico Técnico[editar · editar código]
Artículo principal: Sistema Técnico de Unidades
Longitud: metro (m). La misma definición del Sistema Internacional.
Tiempo: segundo (s).La misma definición del Sistema Internacional.
Fuerza: kilogramo-fuerza (kgf). El peso de una masa de 1 kg (S.I.), en condiciones normales de gravedad (g = 9,80665 m/s2).
Magnitudes físicas derivadas
Artículo principal: Unidades derivadas del SI
Una vez definidas las magnitudes que se consideran básicas, las demás resultan derivadas y se pueden expresar como combinación de las primeras.
Las unidades derivadas se usan para las siguientes magnitudes: superficie, volumen, velocidad, aceleración, densidad, frecuencia, periodo, fuerza, presión, trabajo, calor, energía, potencia, carga eléctrica, diferencia de potencial, potencial eléctrico, resistencia eléctrica, etcétera.
Algunas de las unidades usadas para esas magnitudes derivadas son:
Fuerza: newton (N) que es igual a kg·m/s2
Energía: julio (J) que es igual a kg·m2/s2