ARTÍCULOS REFERENTES A LA UNIDAD # 2

ARTICULO 1

MÉTODO DEL POLÍGONO

Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.

El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.

Suma de Vectores (Metodo del Poligono)

Cuando vamos a sumar más de dos vectores , podemos sumar dos de ellos por el método del triángulo. Luego el vector resultante sumarlo con otro vector también por el método del triángulo, y así sucesivamente hasta llegar a obtener la resultante final.

Otra forma de hacer la suma , es utilizando el llamado método del polígono. Este método es simplemente la extensión del método del triángulo. Es decir, se van desplazando los vectores para colocarlos la “cabeza” del uno con la “cola” del otro (un “trencito”) y la resultante final es el vector que cierra el polígono desde la “cola” que quedo libre hasta la “cabeza” que quedo también libre (cerrar con un “choque de cabezas”). Nuevamente el orden en que se realice la suma no interesa, pues aunque el polígno resultante tiene forma diferente en cada caso, la resultante final conserva su magnitud, su dirección y su sentido.

Reglas para el método del paralelogramo

Las cantidades vectoriales no se suman como las escalares. Una velocidad de 2 Km/h sumada con otra velocidad de 3 Km/h, no necesariamente da como resultado 5 Km/h.

Para encontrar la resultante de dos vectores en un sistema convergente o angular con el método del paralelogramo, primero debes asegurarte de dibujar los vectores con el mismo punto de origen. Acuérdate de dibujarlos a escala.

Luego, con tus escuadras, trazas paralelas a los vectores. ¿Ves lo que construiste? Eso, que quizá te parece un rectángulo “chueco”, es un paralelogramo (que se define como un polígono de cuatro lados, paralelos dos a dos).

Como el cuadrado y el rectángulo son casos particulares del paralelogramo, habrá ocasiones, de vez en cuando, en que al trazar tus vectores y sus líneas paralelas obtengas alguna de estas dos figuras. Pero, por lo general, lo que construirás será un romboide o un rombo. Si necesitas refrescar estos conceptos geométricos, te recomiendo que leas 

La resultante será la diagonal del paralelogramo que salga del punto de origen de los vectores y cuya punta de flecha (acuérdate que es un vector y por lo tanto se representa con una flecha) quede ubicada donde se cruzan las paralelas que dibujaste.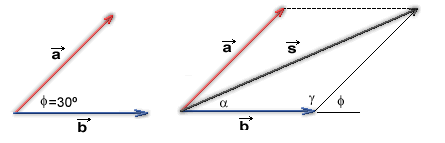

Para saber la magnitud de tu resultante, mides los centímetros que tiene y luego los conviertes a tus unidades usando tu escala… Anota también el ángulo que forma con la línea horizontal donde se encuentra el origen de los vectores y anota el sentido usando las coordenadas (N, S, E, NE, SO, SE, etc.)

ARTICULO 2

CANTIDADES  FISICAS

Vectores: Definición de Cantidades Escalares y Vectoriales

Algunas cantidades quedan totalmente descritas si se expresan con un número y una unidad.

Por ejemplo, una masa de 30 kg. La masa queda totalmente descrita por su magnitud representada por el número (para el caso, 30 es la magnitud) y las unidades correspondientes para la masa: kilogramos. Estas cantidades son escalares.

Definición: Una cantidad escalar se especifica totalmente por su magnitud, que consta de un número y una unidad.

Las operaciones entre cantidades escalares deben ser dimensionalmente coherentes; es decir, las cantidades deben tener las mismas unidades para poder operarse.

30 kg + 40 kg = 70 kg

20 s + 43 s = 63 s

Algunas cantidades escalares comunes son la masa, rapidez, distancia, tiempo, volúmenes, áreas entre otras.

Para el caso de algunas cantidades, no basta con definirlas solo con un número y una cantidad, sino además se debe especificar una dirección y un sentido que las defina completamente. Estas cantidades son vectoriales.

Escalar (física)

Un escalar es un tipo de magnitud física que se expresa por un solo número y tiene el mismo valor para todos los observadores. Por ejemplo, la temperatura de un cuerpo se expresa con una magnitud escalar. Una magnitud física se denomina escalar cuando puede representarse con un único número (única coordenada) invariable en cualquier sistema de referencia. Así la masade un cuerpo es un escalar, pues basta un número para representarla (por ejemplo: 75 kg). Por el contrario una magnitud es vectorial o más generalmente tensorial, cuando se necesita algo más que un número para representarla completamente. Por ejemplo, la velocidad del viento es una magnitud vectorial, ya que además de su módulo (que se mide como una magnitud escalar), debe indicarse también su dirección (norte, sur , este, etc.), que se define por un vector unitario. En cambio, la distribución de tensiones internas de un cuerpo requiere especificar en cada punto una matriz llamada tensor tensión y por tanto el estado de tensión de un cuerpo viene representado por una "magnitud tensorial"

Magnitudes

Las magnitudes son atributos con los que medimos determinadas propiedades físicas, por ejemplo una temperatura, una longitud, una fuerza, la corriente eléctrica, etc. Encontramos dos tipos de magnitudes, las escalares y las vectoriales. 

Magnitudes escalares

Las magnitudes escalares tienen únicamente como variable a un número que representa una determinada cantidad. Por ejemplo la masa de un cuerpo, que se mide en Kilogramos.

Magnitudes vectoriales

En muchos casos las magnitudes escalares no dan información completa sobre una propiedad física. Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones. Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido. Ejemplos de magnitudes vectoriales son la velocidad y la fuerza.

Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.

En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).

Vector

Para otros usos de este término, véase Vector (desambiguación).

Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio vectorial.

Representación gráfica de un vector como unsegmento orientado sobre una recta.

En Física, un vector (también llamado vector euclidiano o vector geométrico) es una herramienta geométrica utilizada para representar unamagnitud física definida por su módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).^1 2 3 Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta dirigidos («flechas») en el plano  o en el espacio .

En Matemáticas se define un vector como un elemento de un espacio vectorial, esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo, la longitud y la orientación (ver espacio vectorial). En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo.

Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección y el sentido (hacia donde se dirige); la fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto.

SUMA Y GRAFICOS DE VECTORES

Gráficamente la suma o RESULTANTE de vectores se obtiene uniendo sucesivamente los extremos y orígenes de ellos, como se muestra en la figura. El vector suma o resultante se obtiene uniendo el primer origen con el último extremo.

En el caso de dos vectores este procedimiento produce un triángulo formado por los vectores y la resultante. Otra forma gráfica de sumar dos vectores consiste en unir los orígenes y trazar líneas auxiliares paralelas a los vectores, que pasen por el extremo del otro.

La resultante es el vector que une los orígenes comunes con la intersección de las paralelas auxiliares (método del paralelogramo).

Note que el orden de la suma no afecta el resultado, mostrando que es conmutativa:

A + B = B + A

Si sumamos los vectores A, B y C de la figura anterior a través del método del paralelogramo, veremos claramente que:

(A + B) + C = A + (B + C)

Mostrando que la suma es asociativa (se recomienda comprobarlo gráficamente). Por otra parte, es innecesaria la definición de resta, pues claramente A – B es la suma de A y el opuesto de B.

A - B = A + (- B)

Si consideramos el paralelogramo que resulta de los vectores A y B y las paralelas auxiliares, observamos que la suma y la resta de ambos vectores constituyen gráficamente las diagonales mayor y menor respectivamente.

Un vector queda definido por su módulo, dirección y sentido: desde A hasta B.