LEYES DE NEWTON Y SIMULADORES

Primera Ley de Newton

concepto:

La primera ley de Newton, conocida también como Ley de inercia nos indica que en ausencia de fuerzas externas un objeto en reposo y un objeto en movimiento continuara en movimiento a velocidad constante. 

Esta ley postula por tanto que un cuerpo no puede cambiar por si solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza neta sobre él. Newton toma en cuenta, sí, que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva.

En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma; un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta

PROBLEMA APLICADO A LA PRIMERA LEY DE NEWTON

Considere los tres bloques conectados que se muestran en el diagrama.

Si el plano inclinado es sin fricción y el sistema esta en equilibrio, determine (en función de m, g y θ).

a) La masa M

b) Las tensiones T1 y T2.

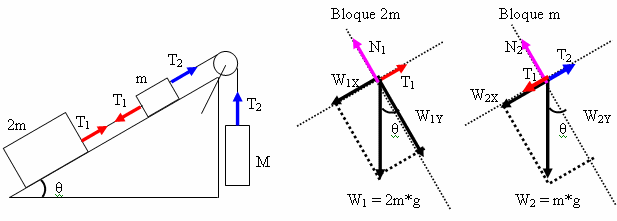
Bloque 2m

∑Fx = 0

T1 – W1X = 0

Pero: W1X = W1 sen θ W1 = 2m*g

W1X = (2m*g) sen θ

Reemplazando

T1 – W1X = 0

T1 – (2m*g) sen θ = 0 (Ecuaciσn 1)

Bloque m

∑Fx = 0

T2 - T1 – W2X = 0

Pero: W2X = W2 sen θ W2 = m*g

W2X = (m*g) sen θ

Reemplazando

T2 - T1 – W2X = 0

T2 - T1 – (m*g) sen θ = 0 (Ecuación 2)

Resolviendo las ecuaciones tenemos:

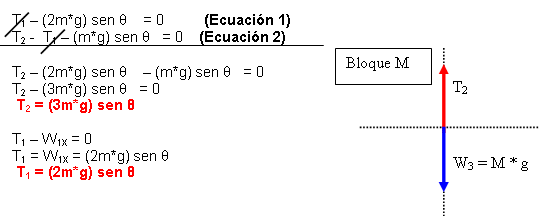
Bloque M

∑FY = 0

T2 – W3 = 0

T2 = W3

W3 = M * g

T2 = M * g

Pero: T2 = (3m*g) sen θ

T2 = M * g

M * g = (3m*g) sen θ

SIMULADOR 1º LEY 

http://ceres.tucansys.com/sco011/Index.htm?e=27&q=1&d=1

SEGUNDA LEY DE NEWTON

CONCEPTO:

La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:

F = m a

Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:

F = m a

La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,

1 N = 1 Kg · 1 m/s2

La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m · a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.

Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

p = m · v

La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg·m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:

La Fuerza que actúa sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,

F = dp/dt

De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para el caso de que la masa sea constante, recordando la definición de cantidad de movimiento y que como se deriva un producto tenemos:

F = d(m·v)/dt = m·dv/dt + dm/dt ·v

Como la masa es constante

dm/dt = 0

y recordando la definición de aceleración, nos queda

F = m a

tal y como habíamos visto anteriormente.

Otra consecuencia de expresar la Segunda ley de Newton usando la cantidad de movimiento es lo que se conoce como Principio de conservación de la cantidad de movimiento. Si la fuerza total que actua sobre un cuerpo es cero, la Segunda ley de Newton nos dice que:

0 = dp/dt

es decir, que la derivada de la cantidad de movimiento con respecto al tiempo es cero. Esto significa que la cantidad de movimiento debe ser constante en el tiempo (la derivada de una constante es cero). Esto es el Principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es nula, la cantidad de movimiento del cuerpo permanece constante en el tiempo.

Problemas de aplicación de la segunda ley de Newton 

Tensión y fuerzas normales 

1. Un hombre de 110 kg baja al suelo desde una altura de 12 m, sosteniéndose de 

una cuerda, que pasa por una polea, y que en su otro extremo tiene unido un saco 

de arena de 74 kg. (a) ¿Con que velocidad cae el hombre al suelo? (b) ¿Hay algo 

que pueda hacer el hombre para reducir la velocidad con la que cae? (c) Calcular 

el valor de la tensión de la cuerda 

Solución: 

(a) Debido a que el movimiento tanto del hombre como del saco de arena ocurre 

en la dirección vertical. En el movimiento del hombre y del saco de arena se 

supone que la dirección positiva del eje y apunta hacia arriba. 

Ley de Newton aplicada al hombre: T – mhg = - mha. 

Ley de Newton aplicada a la caja: T – msg = msa. 

Eliminando T de las dos ecuaciones, se obtiene la aceleración: 

a = (mh – ms)g/( mh + ms) = ((110 - 74) x 9.81)/(110 + 74) = 1.92 m/s2

. 

Velocidad del hombre al llegar al suelo: v = (2ah)0.5 = (2 x 1.92 x 12)0.5 = 6.8 m/s 

(b) Agregar arena al saco. 

(c) Se tiene que T - mhg = -mha. Sustituyendo la expresión para la aceleración a, 

se obtiene que T = mhg - mh(mh – ms)g/( mh + ms) = mhg(1 - (mh – ms)/( mh + ms)). 

Finalmente se obtiene que 

T = 2mhmsg/( mh + ms) = 2(110)(74)(9.81)/(110 + 74) = 868 N. 

¿Qué pasa cuando mS = 0? ¿Cuánto valen a y T? 

¿Qué pasa cuando mS = mh? ¿Cuánto valen a y T? 

2. Un elevador y su carga tienen una masa total de 1600 kg. Calcular la tensión 

del cable que sostiene al elevador cuando se hace que éste, que inicialmente 

descendía a 12 m/s, se detenga con una aceleración constante en 42.0 m. 

Solución: 

La aceleración del elevador es a = (vf 2– vi2)/2x = -122/(2 x 42) = -1.71 m/s2

. 

La tensión es T = mg + ma = m(g + a) = 1600 (9.81 + 1.71) = 18,432 N 

3. Un elevador de 6200 lb es jalado hacia arriba por un cable con una aceleración 

de 3.8 ft/s2

. (a) ¿Cuál es la tensión del cable? 

Solución: 

T = mg + ma = m(g + a) = 6200 x (32 + 3.8) = 221960 lbF

SIMULADOR DE LA 2da LEY

http://ceres.tucansys.com/sco012/Index.htm?e=27&q=1&d=1

TERCERA LEY DE NEWTON

Concepto: 

La tercera ley de Newton explica las fuerzas de acción y reacción. Estas fuerzas las ejercen todos los cuerpos que están en contacto con otro, así un libro sobre la mesa ejerce una fuerza de acción sobre la mesa y la mesa una fuerza de reacción sobre el libro. Estas fuerzas son iguales pero contrarias; es decir tienen el mismo modulo y sentido, pero son opuestas en dirección.

Esto significa que siempre en que un cuerpo ejerce una fuerza sobre otro este también ejerce una fuerza sobre él.

Se nombra fuerza de acción a la que es ejercida por el primer cuerpo que origina una fuerza sobre otro, por lo tanto se denomina fuerza de reacción a la es originada por el cuerpo que recibe y reacciona (De allí el nombre) con esta otra fuerza sobre el primer cuerpo.

¿Pero qué pasa cuando ningún cuerpo origino primariamente la fuerza, como en el ejemplo del libro sobre la mesa? Cualquiera puede ser denominada fuerza de acción y obviamente a la otra se le denominará como fuerza de reacción.

Cuando uno se apoya en la pared, cuando hay un libro sobre la mesa o cuando se empuja un auto hay fuerzas que actúan sobre los cuerpos, y más de las que uno piensa. En el ejemplo del auto claro que hay una fuerza, la de la persona que empuja, pero que sucede con los otros ejemplos. Sobre los cuerpos están actuando muchas fuerzas constantemente como la de gravedad, que es la atracción que ejercen todos los cuerpos sobre los otros; la normal, que es la que evitan que los cuerpos caigan cuando están sobre algo; la de roce, que actúa contra el sentido del movimiento; la de acción y la de reacción. Son estas últimas dos las que son representadas en la tercera ley de Newton. Normalmente en la naturaleza las fuerzas no se presentan solas, sino que en pares como son las fuerzas de acción y reacción.

problemas de la 3 ley

1. Al patear una pelota, el pie ejerce una fuerza sobre ésta; pero, al mismo tiempo, puede sentirse una fuerza en dirección contraria ejercida por la pelota sobre el pie.
2. Si una persona empuja a una pared la pared. La persona ejerce una fuerza sobre la pared y la pared otra fuerza sobre la persona.
3. Cuando una persona camina empuja hacia atrás el suelo, la reacción del suelo es empujarlo hacia adelante, por lo que se origina un movimiento de la persona hacia adelante. Lo mismo sucede con un auto en movimiento, las ruedas empujan el camino y este la empuja hacia adelante.
4. Un objeto colgando de una cuerda ejerce una fuerza sobre la cuerda hacia abajo, pero la cuerda ejerce una fuerza sobre este objeto hacia arriba, dando como resultado que el objeto siga colgando y no caiga.

simulador 3ra ley de Newton 

http://ceres.tucansys.com/sco013/Index.htm?e=27&q=1&d=1

 

SIMULADORES

SIMULADORES
# 1
SIMULADOR DE CAÍDA LIBRE
ESTO ES LO QUE SE LO LLAMA CAÍDA LIBRE SE DICE QUE EN:

En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquial mente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.

El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción des aceleradora de la gravedad, como un disparo vertical; o a satélites en órbita alrededor de la Tierra o de cualquier otro cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.

Ejemplos de caída libre deportiva  en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.

http://www.educaplus.org/play-302-Gr%C3%A1ficas-de-la-ca%C3%ADda-libre.html

# 2
MOVIMIENTO PARABÓLICO

 Se denomina movimiento parabólico al realizado por un objeto  describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.

Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.

http://phet.colorado.edu/sims/projectile-motion/projectile-motion_es.html

#3
MOVIMIENTO RECTILIENO UNIFORME

Un movimiento es rectilíneo cuando un móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.

Movimiento que se realiza sobre una línea recta.

Velocidad constante; implica magnitud y dirección constantes.

La magnitud de la velocidad recibe el nombre de celeridad o rapidez.

Aceleración nula

http://www.educaplus.org/play-350-Movimiento-rectil%C3%ADneo-uniforme.html

# 4

SEGUNDA LEY DE NEWTON

Las leyes de Newton, también conocidas como leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular, aquellos relativos al movimiento de los cuerpos. Revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.

http://ceres.tucansys.com/sco012/Index.htm?e=27&q=1&d=1

# 5

MOVIMIENTO CIRCULAR

En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio y centro fijos y velocidad angular constante.

http://ceres.tucansys.com/Sco010/esp/Index.htm?e=27&q=1&d=1

http://www.ing.uc.edu.ve/~vbarrios/fisica1/fisica1_tutoriales/MovimientoCircular.htm

# 6

RELATIVIDAD

En relatividad, estas magnitudes físicas son representadas por vectores 4-dimensionales o bien por objetos matemáticos llamados tensores, que generalizan los vectores, definidos sobre un espacio de cuatro dimensiones. Matemáticamente estos 4-vectores y 4-tensores son elementos definidos del espacio vectorial tangente al espacio-tiempo (y los tensores se definen y se construyen a partir del fibrado tangente o cotangente de la variedad que representa el espacio-tiempo)

http://ceres.tucansys.com/sco014/Index.htm?e=27&q=1&d=1

# 7

SISTEMAS DE COORDENADAS

En geometría, un sistema de coordenadas es un sistema que utiliza uno o más números (coordenadas) para determinar unívocamente la posición de un punto o de otro objeto geométrico.1 El orden en que se escriben las coordenadas es significativo y a veces se las identifica por su posición en una tupla ordenada; también se las puede representar con letras

http://www.educaplus.org/play-32-Coordenadas-polares-y-cartesianas.html

CINEMATICA

Cinemática

Unidad # 3
Mi opinión :

La cinemática es la rama de la física que estudia las leyes del movimiento de los cuerpos sin considerar las causas que lo originan (las fuerzas) y se limita, esencialmente, al estudio de la trayectoria en función del tiempo. La aceleración es el ritmo con el que cambia la velocidad. La velocidad y la aceleración son las dos principales magnitudes que describen cómo cambia la posición en función del tiempo.

Movimiento rectilíneo

Es aquél en el que el móvil describe una trayectoria en línea recta.

Movimiento rectilíneo uniforme

En este movimiento la velocidad permanece constante y no hay una variación de la aceleración (a) en el transcurso del tiempo. Esto corresponde al movimiento de un objeto lanzado en el espacio fuera de toda interacción, o al movimiento de un objeto que se desliza sin fricción. Siendo la velocidad v constante, la posición variará lineal mente respecto del tiempo, según la ecuación

Movimiento armónico simple

Es un movimiento periódico de vaivén, en el que un cuerpo oscila a un lado y a otro de una posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. Matemáticamente, la trayectoria recorrida se expresa en función del tiempo usando funciones trigonométricas, que son periódicas. Así por ejemplo, la ecuación de posición respecto del tiempo, para el caso de movimiento en una dimensión 

la que corresponde a una función sinusoidal de frecuencia f \,, de amplitud A y fase de inicial \phi \,.

Los movimientos del péndulo, de una masa unida a un muelle o la vibración de los átomos en las redes cristalinas son de estas características.

La aceleración que experimenta el cuerpo es proporcional al desplazamiento del objeto y de dirección contraria, desde el punto de equilibrio. Matemáticamente:

donde k \, es una constante positiva y x \, se refiere a la elongación (desplazamiento del cuerpo desde la posición de equilibrio).

La solución a esa ecuación diferencial lleva a funciones trigonométricas de la forma anterior. Lógicamente, un movimiento periódico oscilatorio real se ralentiza en el tiempo (por fricción mayormente), por lo que la expresión de la aceleración es más complicada, necesitando agregar nuevos términos relacionados con la fricción. Una buena aproximación a la realidad es el estudio del movimiento oscilatorio amortiguado

Movimiento parabólico

El movimiento parabólico se puede analizar como la composición de dos movimientos rectilíneos distintos: uno horizontal (según el eje x) de velocidad constante y otro vertical (según eje y) uniformemente acelerado, con la aceleración gravitatoria; la composición de ambos da como resultado una trayectoria parabólica.

Claramente, la componente horizontal de la velocidad permanece invariable, pero la componente vertical y el ángulo θ cambian en el transcurso del movimiento.

En la figura 4 se observa que el vector velocidad inicial \ v_0  forma un ángulo inicial \ \theta_0 respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:

El desplazamiento horizontal está dado por la ley del movimiento uniforme, por tanto sus ecuaciones

En tanto que el movimiento según el eje \ y  será rectilíneo uniformemente acelerado, siendo sus ecuaciones:

y representa una parábola en el plano y(x). En la figura 4 se muestra esta representación, pero en ella se ha considerado \ y_0=0  (no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad \ v_y  sea nula (máximo de la parábola); y que el alcance horizontal \ x ocurrirá cuando el cuerpo retorne al suelo, en \ y=0  (donde la parábola corta al eje \ x ).

Movimiento circular

El movimiento circular en la práctica es un tipo muy común de movimiento: Lo experimentan, por ejemplo, las partículas de un disco que gira sobre su eje, las de una noria, las de las agujas de un reloj, las de las paletas de un ventilador, etc. Para el caso de un disco en rotación alrededor de un eje fijo, cualquiera de sus puntos describe trayectorias circulares, realizando un cierto número de vueltas durante determinado intervalo de tiempo. Para la descripción de este movimiento resulta conveniente referirse ángulos recorridos; ya que estos últimos son idénticos para todos los puntos del disco (referido a un mismo centro). La longitud del arco recorrido por un punto del disco depende de su posición y es igual al producto del ángulo recorrido por su distancia al eje o centro de giro. La velocidad angular (ω) se define como el desplazamiento angular respecto del tiempo, y se representa mediante un vector perpendicular al plano de rotación; su dirección se determina aplicando la "regla de la mano derecha" o del sacacorchos. La aceleración angular (α) resulta ser variación de velocidad angular respecto del tiempo, y se representa por un vector análogo al de la velocidad angular, pero puede o no tener la misma dirección (según acelere o retarde).

La velocidad (v) de una partícula es una magnitud vectorial cuyo módulo expresa la longitud del arco recorrido (espacio) por unidad de tiempo tiempo; dicho módulo también se denomina rapidez o celeridad. Se representa mediante un vector cuya dirección es tangente a la trayectoria circular y coincide con el del movimiento.

La aceleración (a) de una partícula es una magnitud vectorial que indica la rapidez con que cambia la velocidad respecto del tiempo; esto es, el cambio del vector velocidad por unidad de tiempo. La aceleración tiene generalmente dos componentes: la aceleración tangencial a la trayectoria y la aceleración normal a ésta. La aceleración tangencial es la que causa la variación del módulo de la velocidad (celeridad) respecto del tiempo, mientras que la aceleración normal es la responsable del cambio de dirección de la velocidad. Los módulos de ambas componentes de la aceleración dependen de la distancia a la que se encuentre la partícula respecto del eje de giro.

Movimiento circular uniforme

Se caracteriza por tener una velocidad variable o estructural constante por lo que la aceleración angular es nula. La velocidad lineal de la partícula no varía en módulo, pero sí en dirección. La aceleración tangencial es nula; pero existe aceleración centrípeta (la aceleración normal), que es causante del cambio de dirección.

Matemáticamente, la velocidad angular se expresa

La velocidad es la derivada temporal del vector de posición y la aceleración es la derivada temporal de la velocidad:

o bien sus expresiones integrales:

EXISTEN DOS TIPOS DE MOVIMIENTO, CARACTERIZADOS POR SU TRAYECTORIA, DE ESTA CATEGORÍA:

Magnitud física

Una magnitud física es una propiedad o cualidad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición o una relación de medidas. Las magnitudes físicas se miden usando un patrón que tenga bien definida esa magnitud, y tomando como unidad la cantidad de esa propiedad que posea el objeto patrón. Por ejemplo, se considera que el patrón principal de longitud es el metro en el Sistema Internacional de Unidades.

Las primeras magnitudes definidas estaban relacionadas con la medición de longitudes, áreas, volúmenes, masas patrón, y la duración de periodos de tiempo.

Existen magnitudes básicas y derivadas, y constituyen ejemplos de magnitudes físicas: la masa, la longitud, el tiempo, la carga eléctrica, la densidad, la temperatura, la velocidad, la aceleración y la energía. En términos generales, es toda propiedad de los cuerpos o sistemas que puede ser medida. De lo dicho se desprende la importancia fundamental del instrumento de medición en la definición de la magnitud.1

La Oficina Internacional de Pesos y Medidas, por medio del Vocabulario Internacional de Metrología (International Vocabulary of Metrology, VIM), define a la magnitud como un atributo de un fenómeno, un cuerpo o sustancia que puede ser distinguido cualitativamente y determinado cuantitativamente.2

A diferencia de las unidades empleadas para expresar su valor, las magnitudes físicas se expresan en cursiva: así, por ejemplo, la "masa" se indica con "m", y "una masa de 3 kilogramos" la expresaremos como m = 3 kg. 

Magnitudes escalares, vectoriales y tensoriales

Las magnitudes escalares son aquellas que quedan completamente definidas por un número y las unidades utilizadas para su medida. Esto es, las magnitudes escalares están representadas por el ente matemático más simple, por un número. Podemos decir que poseen un módulo, pero que carecen de dirección. Su valor puede ser independiente del observador (v.g.: la masa, la temperatura, la densidad, etc.) o depender de la posición (v.g.: la energía potencial), o estado de movimiento del observador (v.g.: la energía cinética).

Las magnitudes vectoriales son aquellas que quedan caracterizadas por una cantidad (intensidad o módulo), una dirección y un sentido. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa mediante un segmento orientado. Ejemplos de estas magnitudes son: la velocidad, la aceleración, la fuerza, el campo eléctrico, intensidad luminosa, etc.

Además, al considerar otro sistema de coordenadas asociado a un observador con diferente estado de movimiento o de orientación, las magnitudes vectoriales no presentan invariancia de cada uno de los componentes del vector y, por tanto, para relacionar las medidas de diferentes observadores se necesitan relaciones de transformación vectorial. En mecánica clásica también el campo electrostático se considera un vector; sin embargo, de acuerdo con la teoría de la relatividad esta magnitud, al igual que el campo magnético, debe ser tratada como parte de una magnitud tensorial.

Las magnitudes tensoriales son las que caracterizan propiedades o comportamientos físicos modelizables mediante un conjunto de números que cambian tensorialmente al elegir otro sistema de coordenadas asociado a un observador con diferente estado de movimiento (marco móvil) o de orientación.

De acuerdo con el tipo de magnitud, debemos escoger leyes de transformación (por ej. la transformación de Lorentz) de las componentes físicas de las magnitudes medidas, para poder ver si diferentes observadores hicieron la misma medida o para saber qué medidas obtendrá un observador, conocidas las de otro cuya orientación y estado de movimiento respecto al primero sean conocidos.

Magnitudes extensivas e intensivas

Una magnitud extensiva es una magnitud que depende de la cantidad de sustancia que tiene el cuerpo o sistema. Las magnitudes extensivas son aditivas. Si consideramos un sistema físico formado por dos partes o subsistemas, el valor total de una magnitud extensiva resulta ser la suma de sus valores en cada una de las dos partes. Ejemplos: la masa y el volumen de un cuerpo o sistema, la energía de un sistema termodinámico, etc.

Una magnitud intensiva es aquella cuyo valor no depende de la cantidad de materia del sistema. Las magnitudes intensivas tiene el mismo valor para un sistema que para cada una de sus partes consideradas como subsistemas. Ejemplos: la densidad, la temperatura y la presión de un sistema termodinámico en equilibrio.

En general, el cociente entre dos magnitudes extensivas da como resultado una magnitud intensiva. Ejemplo: masa dividida por volumen representa densidad.

Representación covariante y contravariante

Las magnitudes tensoriales de orden igual o superior a uno admiten varias formas de representación tensorial según el número de índices contravariantes y covariantes. Esto no es muy importante si el espacio es euclídeo y se emplean coordenadas cartesianas, aunque si el espacio no es euclídeo o se usan coordenadas no cartesianas es importante distinguir entre diversas representaciones tensoriales que físicamente representan la misma magnitud. En relatividad general dado que en general el espacio-tiempo es curvo el uso de representaciones convariantes y cotravariantes es inevitable.

Así un vector puede ser representado mediante una tensor 1-covariante o mediante un tensor 1-contravariante. Más generalmente, una magnitud tensorial de orden k admite 2k representaciones tensoriales esencialmente equivalentes. Esto se debe a que en un espacio físico representable mediante una variedad riemanniana (o semiriemanninana como en el caso relativista) existe un isomorfismo entre tensores de tipo \scriptstyle (m,n) y los de tipo \scriptstyle (m',n') siempre y cuando \scriptstyle m+n = m'+n'. El paso de una representación a otra de otro tipo se lleva a cabo mediante la operación de "bajar y subir índices".

Magnitudes objetivas y no objetiva

Una magnitud se dice objetiva si las medidas de dicha magnitud por observadores diferentes pueden relacionarse de manera sistemática. En el contexto de la mecánica newtoniana se restringe el tipo de observador, y se considera que una magnitud es objetiva si se pueden relacionar sistemáticamente las medidas de dos observadores cuyo movimiento relativo en un instante dado es un movimiento de sólido rígido. Existen buenos argumentos para sostener que una ley física adecuada debe estar formulada en términos de magnitudes físicas objetivas. En el contexto de la teoría de la relatividad la objetividad física se amplia al concepto de covariancia de Lorentz (en relatividad especial) y covariancia general (en relatividad especial).

Sistema Internacional de Unidades

Artículo principal: Sistema Internacional de Unidades

El Sistema Internacional de Unidades se basa en dos tipos de magnitudes físicas:

Las siete que toma como unidades fundamentales, de las que derivan todas las demás. Son longitud, tiempo, masa, intensidad de corriente eléctrica, temperatura, cantidad de sustancia e intensidad luminosa.

Las unidades derivadas, que son las restantes y que pueden ser expresadas con una combinación matemática de las anteriores.

Unidades básicas o fundamentales del Sistema Internacional de Unidades[editar · editar código]

Artículo principal: Unidades básicas del SI

Las magnitudes básicas no derivadas del SI son las siguientes:

Longitud: metro (m). El metro es la distancia recorrida por la luz en el vacío en 1/299 792 458 segundos. Este patrón fue establecido en el año 1983.

Tiempo: segundo (s). El segundo es la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del cesio-133. Este patrón fue establecido en el año 1967.

Masa: kilogramo (kg). El kilogramo es la masa de un cilindro de aleación de Platino-Iridio depositado en la Oficina Internacional de Pesas y Medidas. Este patrón fue establecido en el año 1887.

Intensidad de corriente eléctrica: amperio (A). El amperio o ampere es la intensidad de una corriente constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno de otro, en el vacío, produciría una fuerza igual a 2×10-7 newton por metro de longitud.

Temperatura: kelvin (K). El kelvin es la fracción 1/273,16 de la temperatura del punto triple del agua.

Cantidad de sustancia: mol (mol). El mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 12 gramos de carbono-12.

Intensidad luminosa: candela (cd). La candela es la unidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540×1012 Hz y cuya intensidad energética en dicha dirección es 1/683 vatios por estereorradián.

Unidades Fundamentales en el Sistema Cegesimal C.G.S.[editar · editar código]

Artículo principal: Sistema Cegesimal de Unidades

Longitud: centímetro (cm): 1/100 del metro (m) S.I.

Tiempo: segundo (s): La misma definición del S.I.

Masa: gramo (g): 1/1000 del kilogramo (kg) del S.I.

Unidades Fundamentales en el Sistema Gravitacional Métrico Técnico[editar · editar código]

Artículo principal: Sistema Técnico de Unidades

Longitud: metro (m). La misma definición del Sistema Internacional.

Tiempo: segundo (s).La misma definición del Sistema Internacional.

Fuerza: kilogramo-fuerza (kgf). El peso de una masa de 1 kg (S.I.), en condiciones normales de gravedad (g = 9,80665 m/s2).

Magnitudes físicas derivadas

Artículo principal: Unidades derivadas del SI

Una vez definidas las magnitudes que se consideran básicas, las demás resultan derivadas y se pueden expresar como combinación de las primeras.

Las unidades derivadas se usan para las siguientes magnitudes: superficie, volumen, velocidad, aceleración, densidad, frecuencia, periodo, fuerza, presión, trabajo, calor, energía, potencia, carga eléctrica, diferencia de potencial, potencial eléctrico, resistencia eléctrica, etcétera.

Algunas de las unidades usadas para esas magnitudes derivadas son:

Fuerza: newton (N) que es igual a kg·m/s2

Energía: julio (J) que es igual a kg·m2/s2

ARTÍCULOS REFERENTES A LA UNIDAD # 2

ARTICULO 1

MÉTODO DEL POLÍGONO

Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.

El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.

Suma de Vectores (Metodo del Poligono)

Cuando vamos a sumar más de dos vectores , podemos sumar dos de ellos por el método del triángulo. Luego el vector resultante sumarlo con otro vector también por el método del triángulo, y así sucesivamente hasta llegar a obtener la resultante final.

Otra forma de hacer la suma , es utilizando el llamado método del polígono. Este método es simplemente la extensión del método del triángulo. Es decir, se van desplazando los vectores para colocarlos la “cabeza” del uno con la “cola” del otro (un “trencito”) y la resultante final es el vector que cierra el polígono desde la “cola” que quedo libre hasta la “cabeza” que quedo también libre (cerrar con un “choque de cabezas”). Nuevamente el orden en que se realice la suma no interesa, pues aunque el polígno resultante tiene forma diferente en cada caso, la resultante final conserva su magnitud, su dirección y su sentido.

Reglas para el método del paralelogramo

Las cantidades vectoriales no se suman como las escalares. Una velocidad de 2 Km/h sumada con otra velocidad de 3 Km/h, no necesariamente da como resultado 5 Km/h.

Para encontrar la resultante de dos vectores en un sistema convergente o angular con el método del paralelogramo, primero debes asegurarte de dibujar los vectores con el mismo punto de origen. Acuérdate de dibujarlos a escala.

Luego, con tus escuadras, trazas paralelas a los vectores. ¿Ves lo que construiste? Eso, que quizá te parece un rectángulo “chueco”, es un paralelogramo (que se define como un polígono de cuatro lados, paralelos dos a dos).

Como el cuadrado y el rectángulo son casos particulares del paralelogramo, habrá ocasiones, de vez en cuando, en que al trazar tus vectores y sus líneas paralelas obtengas alguna de estas dos figuras. Pero, por lo general, lo que construirás será un romboide o un rombo. Si necesitas refrescar estos conceptos geométricos, te recomiendo que leas 

La resultante será la diagonal del paralelogramo que salga del punto de origen de los vectores y cuya punta de flecha (acuérdate que es un vector y por lo tanto se representa con una flecha) quede ubicada donde se cruzan las paralelas que dibujaste.

Para saber la magnitud de tu resultante, mides los centímetros que tiene y luego los conviertes a tus unidades usando tu escala… Anota también el ángulo que forma con la línea horizontal donde se encuentra el origen de los vectores y anota el sentido usando las coordenadas (N, S, E, NE, SO, SE, etc.)

ARTICULO 2

CANTIDADES  FISICAS

Vectores: Definición de Cantidades Escalares y Vectoriales

Algunas cantidades quedan totalmente descritas si se expresan con un número y una unidad.

Por ejemplo, una masa de 30 kg. La masa queda totalmente descrita por su magnitud representada por el número (para el caso, 30 es la magnitud) y las unidades correspondientes para la masa: kilogramos. Estas cantidades son escalares.

Definición: Una cantidad escalar se especifica totalmente por su magnitud, que consta de un número y una unidad.

Las operaciones entre cantidades escalares deben ser dimensionalmente coherentes; es decir, las cantidades deben tener las mismas unidades para poder operarse.

30 kg + 40 kg = 70 kg

20 s + 43 s = 63 s

Algunas cantidades escalares comunes son la masa, rapidez, distancia, tiempo, volúmenes, áreas entre otras.

Para el caso de algunas cantidades, no basta con definirlas solo con un número y una cantidad, sino además se debe especificar una dirección y un sentido que las defina completamente. Estas cantidades son vectoriales.

Escalar (física)

Un escalar es un tipo de magnitud física que se expresa por un solo número y tiene el mismo valor para todos los observadores. Por ejemplo, la temperatura de un cuerpo se expresa con una magnitud escalar. Una magnitud física se denomina escalar cuando puede representarse con un único número (única coordenada) invariable en cualquier sistema de referencia. Así la masade un cuerpo es un escalar, pues basta un número para representarla (por ejemplo: 75 kg). Por el contrario una magnitud es vectorial o más generalmente tensorial, cuando se necesita algo más que un número para representarla completamente. Por ejemplo, la velocidad del viento es una magnitud vectorial, ya que además de su módulo (que se mide como una magnitud escalar), debe indicarse también su dirección (norte, sur , este, etc.), que se define por un vector unitario. En cambio, la distribución de tensiones internas de un cuerpo requiere especificar en cada punto una matriz llamada tensor tensión y por tanto el estado de tensión de un cuerpo viene representado por una "magnitud tensorial"

Magnitudes

Las magnitudes son atributos con los que medimos determinadas propiedades físicas, por ejemplo una temperatura, una longitud, una fuerza, la corriente eléctrica, etc. Encontramos dos tipos de magnitudes, las escalares y las vectoriales. 

Magnitudes escalares

Las magnitudes escalares tienen únicamente como variable a un número que representa una determinada cantidad. Por ejemplo la masa de un cuerpo, que se mide en Kilogramos.

Magnitudes vectoriales

En muchos casos las magnitudes escalares no dan información completa sobre una propiedad física. Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones. Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido. Ejemplos de magnitudes vectoriales son la velocidad y la fuerza.

Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.

En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).

Vector

Para otros usos de este término, véase Vector (desambiguación).

Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio vectorial.

Representación gráfica de un vector como unsegmento orientado sobre una recta.

En Física, un vector (también llamado vector euclidiano o vector geométrico) es una herramienta geométrica utilizada para representar unamagnitud física definida por su módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).^1 2 3 Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta dirigidos («flechas») en el plano  o en el espacio .

En Matemáticas se define un vector como un elemento de un espacio vectorial, esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo, la longitud y la orientación (ver espacio vectorial). En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo.

Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección y el sentido (hacia donde se dirige); la fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto.

SUMA Y GRAFICOS DE VECTORES

Gráficamente la suma o RESULTANTE de vectores se obtiene uniendo sucesivamente los extremos y orígenes de ellos, como se muestra en la figura. El vector suma o resultante se obtiene uniendo el primer origen con el último extremo.

En el caso de dos vectores este procedimiento produce un triángulo formado por los vectores y la resultante. Otra forma gráfica de sumar dos vectores consiste en unir los orígenes y trazar líneas auxiliares paralelas a los vectores, que pasen por el extremo del otro.

La resultante es el vector que une los orígenes comunes con la intersección de las paralelas auxiliares (método del paralelogramo).

Note que el orden de la suma no afecta el resultado, mostrando que es conmutativa:

A + B = B + A

Si sumamos los vectores A, B y C de la figura anterior a través del método del paralelogramo, veremos claramente que:

(A + B) + C = A + (B + C)

Mostrando que la suma es asociativa (se recomienda comprobarlo gráficamente). Por otra parte, es innecesaria la definición de resta, pues claramente A – B es la suma de A y el opuesto de B.

A - B = A + (- B)

Si consideramos el paralelogramo que resulta de los vectores A y B y las paralelas auxiliares, observamos que la suma y la resta de ambos vectores constituyen gráficamente las diagonales mayor y menor respectivamente.

Un vector queda definido por su módulo, dirección y sentido: desde A hasta B.